É muito
frequente o aparecimento dos
números em sequência retangulares
ordenadas, conhecidas como matrizes na matemática e suas aplicações.
É chamada de matriz m x n no conjunto dos números
reais R, onde m e n são números inteiros maiores ou iguais a 1, a tabela
formada por m x n elementos aij, í = 1,2,3...,m e j = 1,2,3...,n que são
dispostos em m linhas e n colunas ( i são linhas e j são colunas).
Representação genérica de uma matriz
Obs 1: Essa é a representação genérica de uma
matriz A do tipo m x n.
Obs 2: É chamada de matriz m x n, toda tabela de
números dispostos em m linhas e n colunas; essas tabelas devem ser
representadas entre parêntese ( ), colchetes [ ] ou barras duplas // // (na
vertical).
Os elementos da A = aij ( símbolo da matriz acima
) em que i é i-énesima linha e j é j-ésima coluna, podem ser representada pela
notação abaixo:
Obs: Como a representação da matriz genérica é
muito extensa ela pode ser representada pela essa segunda notação.
Tipos de matrizes
Em alguns casos damos denotações especiais para
algumas matrizes, isso pelo motivo da quantidade de linhas ou colunas, ou ainda, pela
distribuição de seus elementos possuírem propriedades que as diferenciam de uma
matriz arbitrária.
Matriz coluna e matriz linha
Uma matriz coluna tem apenas uma coluna, observe:
É uma matriz 3 x 1 ( 3 é linhas e 1 é coluna)
Uma matriz linha tem apenas uma linha, observe:
É uma matriz 1 x 3 ( 1 é linha e 3 é coluna)
Matriz quadrada
Uma matriz é quadrada quando o número de linhas é
igual ao número de colunas, ou seja, m = n.
É uma matriz 3 x 3 ( 3 é coluna e 3 é linha )
Obs 1: Matrizes 1 x 1 ( 1 x 1 é uma matriz
quadrada de ordem 1), 2 x 2, 3 x 3 e 4 x 4 são matrizes quadradas, pois m = n.
Obs 2: os
números -2, 9 e 4 na matriz B formam a diagonal principal e
os números 5, 9 e 1 na matriz B formam a diagonal secundária.
Matriz triangular
Seja uma matriz quadrada de ordem n, se os
elementos abaixo ou
acima da diagonal principal dessa matriz
forem todos nulos, tal matriz é uma matriz triangular.
Veja:
Obs: toda matriz triangular é quadrada,
entretanto nem toda matriz quadrada é triangular.
Matriz
diagonal
Seja uma matriz
quadrada de ordem n, se os elementos abaixo e acima da diagonal principal dessa matriz forem todos
nulo, tal matriz é uma matriz diagonal.
obs: todos os
elementos acima e abaixo da diagonal principal devem ser iguais a zero.
Matriz nula
Quando uma matriz m x n tem todos os seus
elementos iguais a zero, essa matriz é denominada de matriz nula.
Obs: Uma matriz nula e representada por Om
x n ( m é linha e n é coluna )
Exemplos de matrizes nulas:
Exemplo 2

Matriz oposta
Um matriz oposta de uma matriz B de ordem m x n
(m é linha e n é coluna) é uma matriz –B
de mesma ordem, cujos elementos são opostos dos elementos de B.
A oposta é
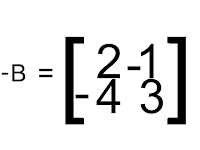
Matriz transposta
Seja a matriz B de ordem mxn, representamos a matriz transposta de B por B^t de ordem invertida nxm. Dessa maneira concluímos que para transformar uma matriz em uma matriz transposta, basta trocar os elementos das linhas pelos elementos das colunas ou vice-versa.
Exemplos:
1)
2)
Matriz identidade
Um matriz identidade
de ordem n, é indicada por In.
Obs 1: Uma matriz identidade é matriz quadrada.
Obs 2: Todas as matrizes quadrada de ordem n em
que os elementos da diagonal principal são iguais a 1 e os outros elementos são
iguais a zero e chamada de matriz identidade.
Igualdade de matrizes
Seja duas matrizes do mesmo tipo A = (aij) mxn e
B = (bij) mxn, A = B se, somente se, todo elemento de A é igual ao seu
correspondente em B.
Observe que a matriz A e B são de mesma ordem m x
n =
3 X 2 ( três linhas e duas colunas ), nas duas
matrizes consideradas temos os seguintes elementos correspondentes a11 e b11, a21 e b21, a31 e b31; a12 e b12,
a22 e b22, a 32 e b32.
Observe que as matrizes são quadradas de ordem 2
e os elementos correspondentes são iguais.
Observe que essas matrizes tem a mesma ordem m x
n = 2 x 2, entretanto os elementos correspondentes
não são iguais.
por: Dan. S.